或许大家都习惯了使用Adam和AdamW,但是我们真的有了解这些优化器的内部原理吗?
优化器的基本思想是梯度下降法,梯度下降法的公式非常简单,
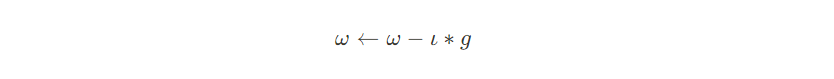
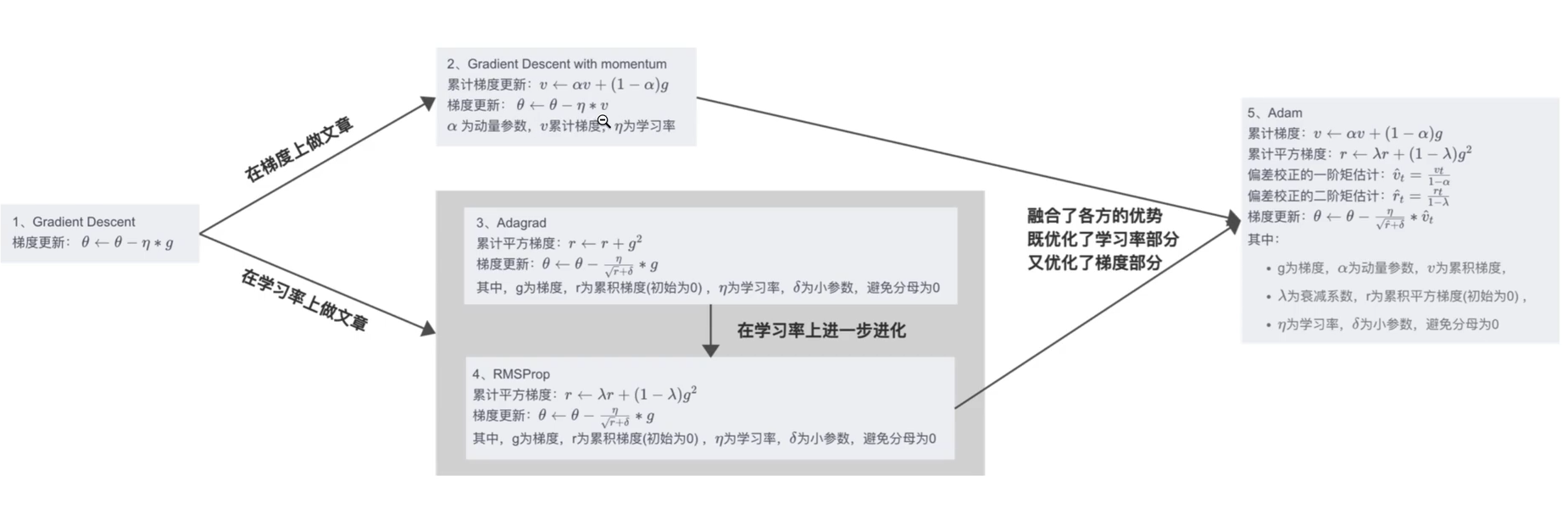
故能修改的地方只有学习率和梯度值,由此催生出3类优化器:
- 1 修改梯度:SGD
- 2 修改学习率:Adagrad,RMSProp
- 3 修改梯度和学习率:Adam,AdamW
详细进化表如下:
1 梯度下降法
1.1 基本思想
先设定一个学习率$\iota$,参数沿梯度的反方向移动。假设需要更新的参数为$\omega$,梯度为g,更新策略为:
$$ \omega \gets \omega -\iota *g $$
1.2 梯度下降法的三种形式
- BGD:批量梯度下降,每次参数更新使用全部的样本
- SGD:随机梯度下降,每次参数更新使用一个样本
- MBGD:小批量梯度下降,每次参数更新使用一部分样本
参数优化步骤:求梯度 → 求梯度平均值 → 更新权重
1.3 优缺点
优点:
- 算法简介,当学习率合适的时候,可以收敛到全局最优(凸函数)
缺点:
- 1 对超参数比较敏感;过小导致收敛速度慢,过大导致越过极值点
- 2 学习率容易在迭代过程中保持不变,被卡在按点
- 3 容易陷入局部极小值
1.4 一维梯度下降法
以目标函数$f(x) = x^2$为例子,看梯度下降法如何工作。
import numpy as np
import matplotlib.pyplot as plt
lrs = [0.05, 0.1, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2]
result = []
for lr in lrs:
x = 10
temp = [x]
for i in range(10):
x -= lr * 2 * x
temp.append(x)
result.append(temp)
fx = np.arange(-10, 10, 0.1)
fig, ax = plt.subplots(2, 4, figsize=(20, 8))
for i in range(2):
for j in range(4):
ax[i][j].plot(fx, [x*x for x in fx])
ax[i][j].plot(result[2*i+j], [x*x for x in result[2*i+j]], "-o")
ax[i][j].set_title(f"learning rate is {lrs[2*i + j]}")
ax[i][j].set_xlabel("x")
ax[i][j].set_ylabel("f(x)")
plt.show()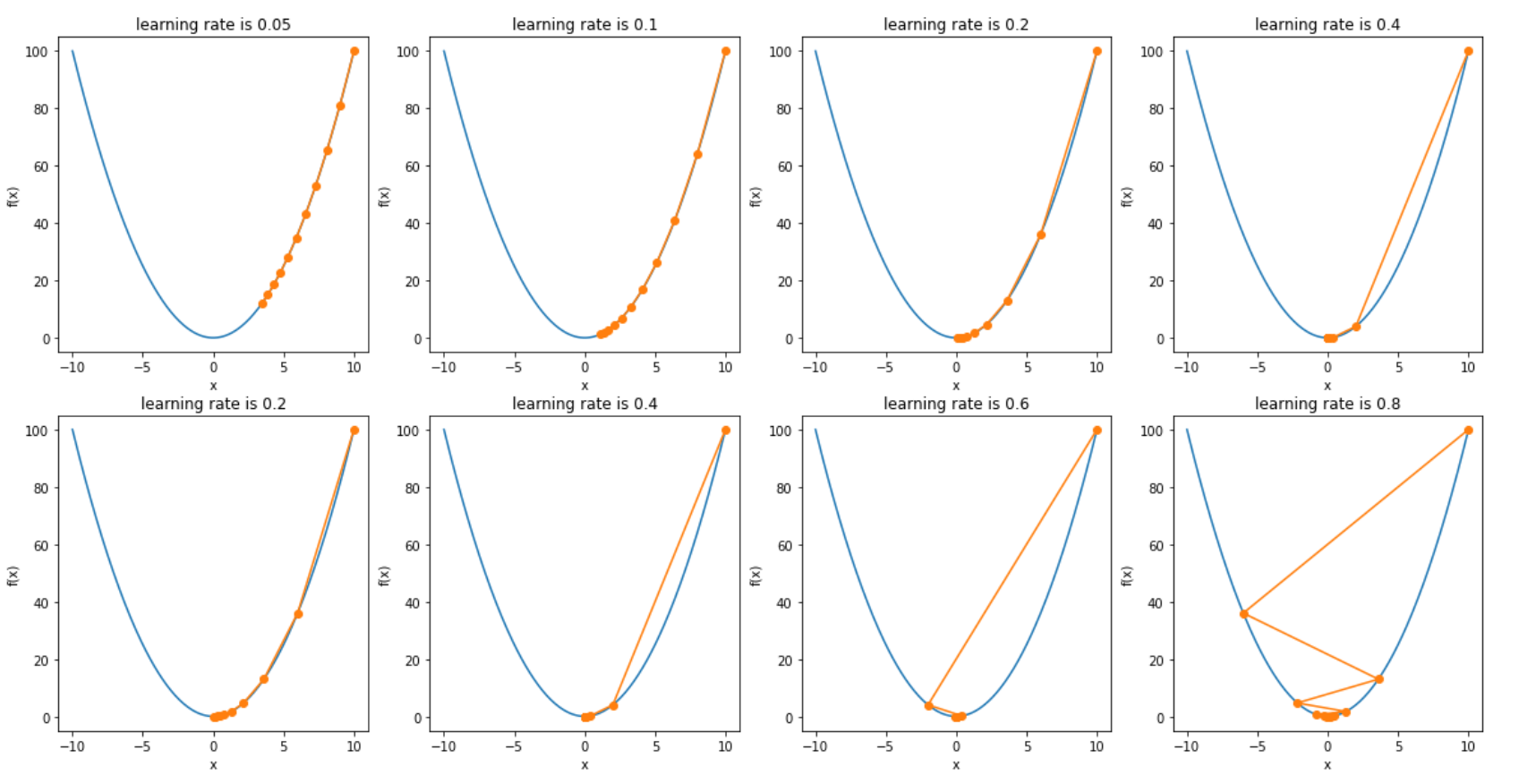
1.5 多维梯度下降法
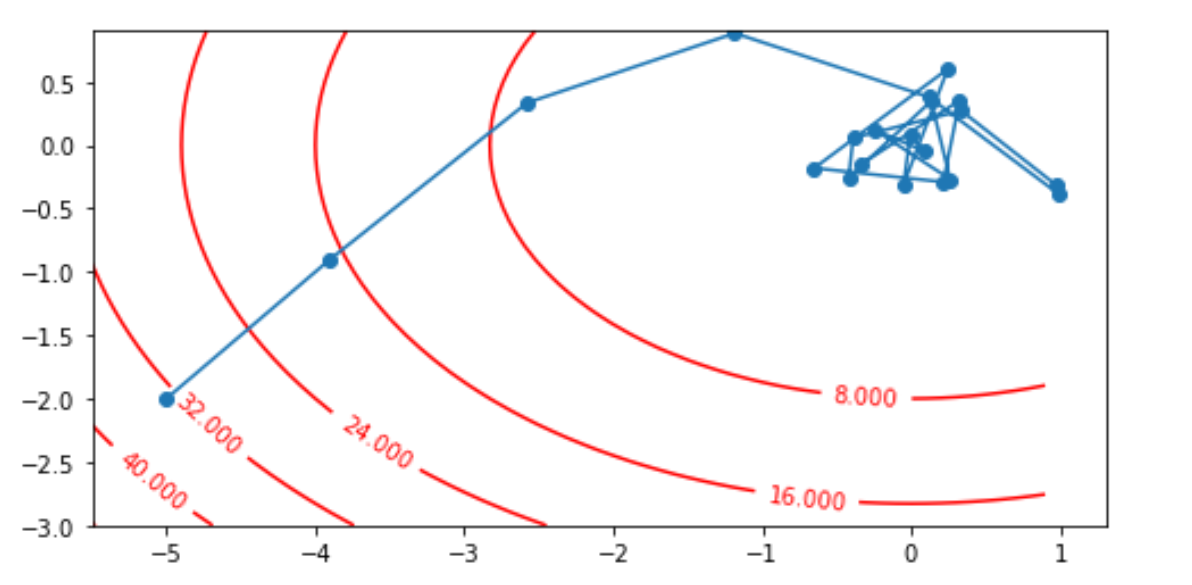
以目标函数$f(x) = x_{1}^2+2x_{2}^2$为例子,使用梯度下降法,观察x1,x2如何从初始位置[-5, -2]的更新轨迹。
import numpy as np import matplotlib.pyplot as plt def loss_func(x1, x2): return x1**2 + 2*x2**2 x1, x2 = -5, -2 eta = 0.4 num_epochs = 20 result = [(x1, x2)] for epoch in range(num_epochs): grad_1 = 2 * x1 grad_2 = 4 * x2 x1 -= eta * grad_1 x2 -= eta * grad_2 result.append((x1, x2)) plt.figure(figsize=(8, 4)) plt.plot(*zip(*result), "-o") x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1)) C = plt.contour(x1, x2, loss_func(x1, x2), colors="red") plt.clabel(C, inline=True, fontsize=10) # ax1 = plt.axes(projection='3d') # ax1.scatter3D(x1, x2, loss_func(x1, x2), cmap='Blues') plt.show()
2 动量
2.1 基本思想
让参数的更新具有惯性,每一步更新都是由前面梯度的累计v和当前梯度g组合而成。
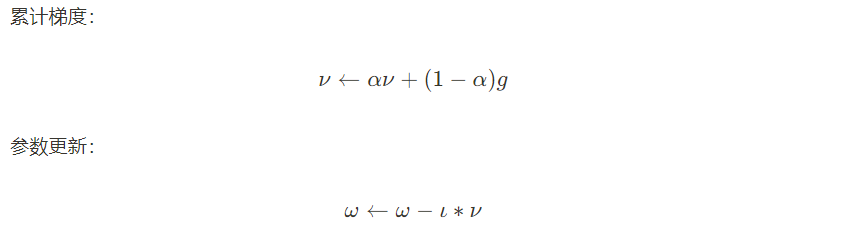
2.2 优缺点
优点:使用梯度的惯性使节点能突破极值点。
import numpy as np
import matplotlib.pyplot as plt
def loss_func(x1, x2):
return x1**2 + 2*x2**2
x1, x2 = -5, -2
v1, v2 = 0, 0
eta, alpha = 0.4, 0.5
num_epochs = 20
result = [(x1, x2)]
for epoch in range(num_epochs):
grad_1 = 2 * x1
grad_2 = 4 * x2
v1 = alpha * v1 + (1-alpha) * grad_1
v2 = alpha * v2 + (1-alpha) * grad_2
x1 -= eta * v1
x2 -= eta * v2
result.append((x1, x2))
plt.figure(figsize=(8, 4))
plt.plot(*zip(*result), "-o")
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
C = plt.contour(x1, x2, loss_func(x1, x2), colors="red")
plt.clabel(C, inline=True, fontsize=10)
# ax1 = plt.axes(projection='3d')
# ax1.scatter3D(x1, x2, loss_func(x1, x2), cmap='Blues')
plt.show()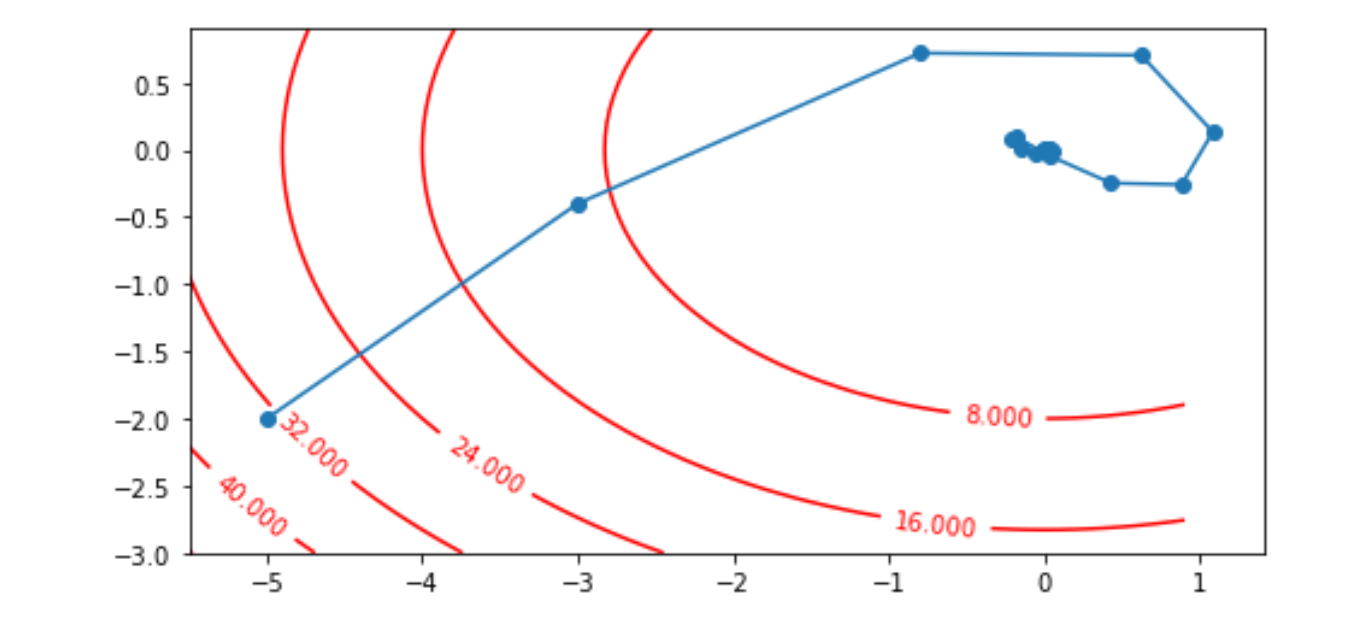
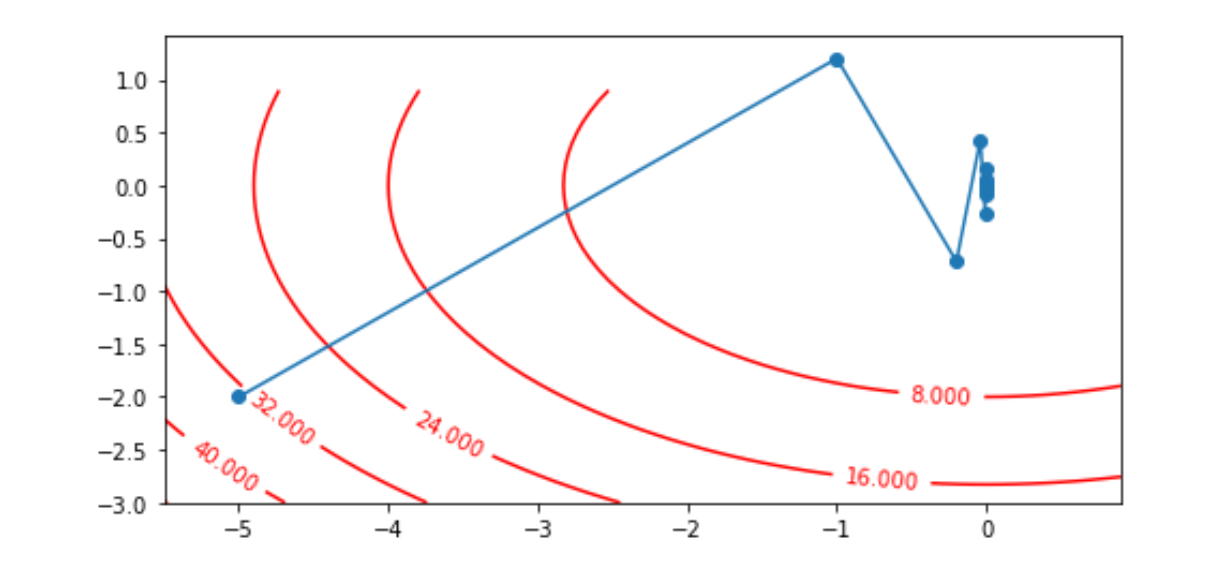
3 Adagrad
3.1 基本思想
自适应学习率优化算法
思想:随机梯度下降法,针对所有的参数,都是使用相同的固定的学习率进行优化,但是不同的采纳数的梯度差异可能很大,使用相同的学习率效果不会很好,针对不同的参数,设置不同的学习率。
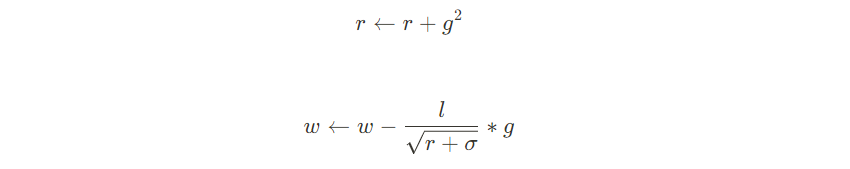
3.2 优缺点
import numpy as np
import matplotlib.pyplot as plt
def loss_func(x1, x2):
return x1**2 + 2*x2**2
x1, x2 = -5, -2
r1, r2 = 0, 0
eta = 0.4
num_epochs = 20
result = [(x1, x2)]
for epoch in range(num_epochs):
grad_1 = 2 * x1
grad_2 = 4 * x2
r1 = r1 + grad_1**2
r2 = r2 + grad_2**2
x1 -= (eta / np.sqrt(r1 + 1e-10)) * grad_1
x2 -= (eta / np.sqrt(r2 + 1e-10))* ( grad_2)
print(f"x1 lr ", (eta / np.sqrt(r1 + 1e-10)))
print(f"x2 lr ", (eta / np.sqrt(r2 + 1e-10)))
result.append((x1, x2))
plt.figure(figsize=(8, 4))
plt.plot(*zip(*result), "-o")
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
C = plt.contour(x1, x2, loss_func(x1, x2), colors="red")
plt.clabel(C, inline=True, fontsize=10)
# ax1 = plt.axes(projection='3d')
# ax1.scatter3D(x1, x2, loss_func(x1, x2), cmap='Blues')
plt.show()
4 RMSProp
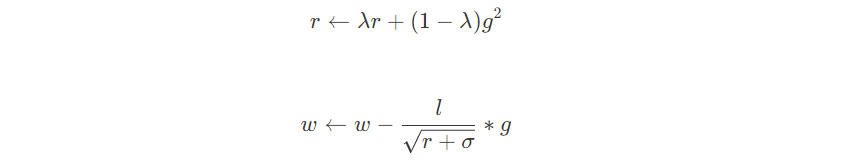
import numpy as np
import matplotlib.pyplot as plt
def loss_func(x1, x2):
return x1**2 + 2*x2**2
x1, x2 = -5, -2
r1, r2 = 0, 0
eta, alpha = 0.4, 0.5
num_epochs = 20
result = [(x1, x2)]
for epoch in range(num_epochs):
grad_1 = 2 * x1
grad_2 = 4 * x2
r1 = alpha * r1 + (1 - alpha) * grad_1**2
r2 = alpha * r2 + (1 - alpha) * grad_2**2
x1 -= (eta / np.sqrt(r1 + 1e-10)) * grad_1
x2 -= (eta / np.sqrt(r2 + 1e-10))* ( grad_2)
# print(f"x1 lr ", (eta / np.sqrt(r1 + 1e-10)))
# print(f"x2 lr ", (eta / np.sqrt(r2 + 1e-10)))
result.append((x1, x2))
plt.figure(figsize=(8, 4))
plt.plot(*zip(*result), "-o")
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
C = plt.contour(x1, x2, loss_func(x1, x2), colors="red")
plt.clabel(C, inline=True, fontsize=10)
# ax1 = plt.axes(projection='3d')
# ax1.scatter3D(x1, x2, loss_func(x1, x2), cmap='Blues')
plt.show()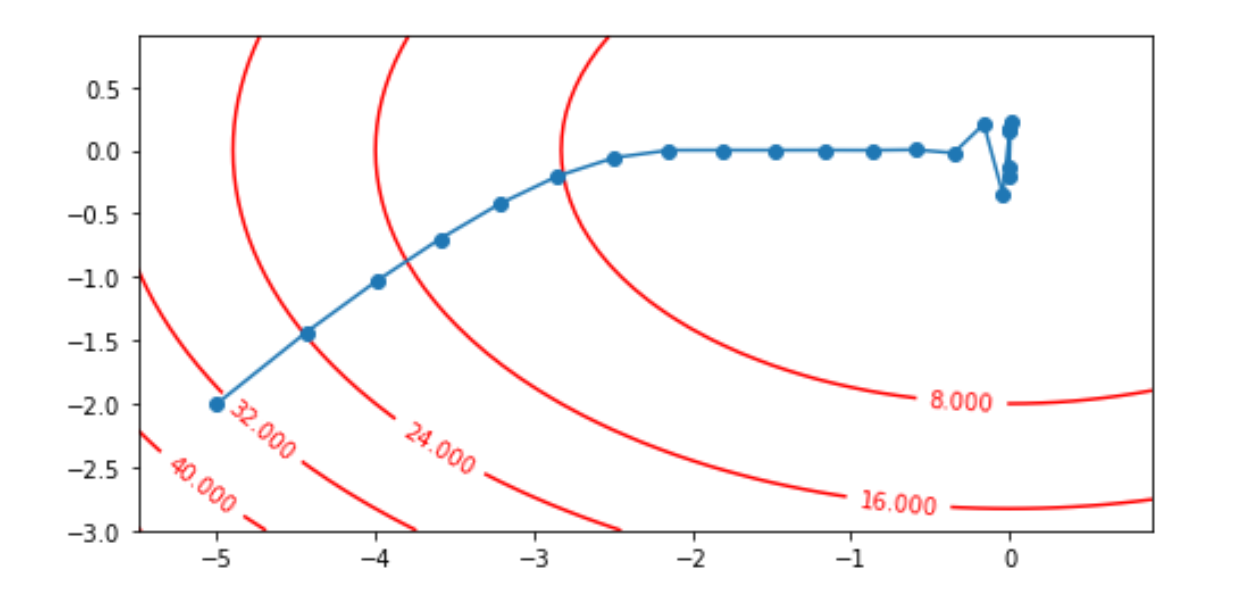
5 Adam
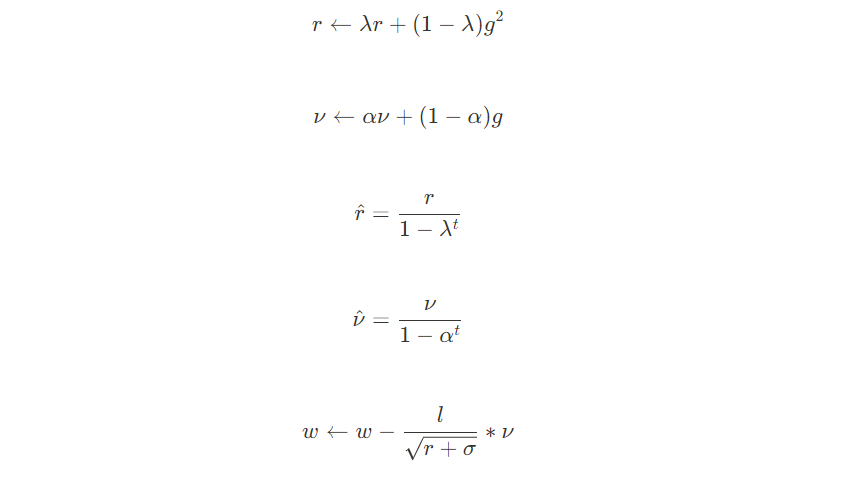
import numpy as np
import matplotlib.pyplot as plt
def loss_func(x1, x2):
return x1**2 + 2*x2**2
x1, x2 = -5, -2
r1, r2 = 0, 0
eta, alpha = 0.4, 0.5
num_epochs = 20
result = [(x1, x2)]
for epoch in range(num_epochs):
grad_1 = 2 * x1
grad_2 = 4 * x2
r1 = alpha * r1 + (1 - alpha) * grad_1**2
r2 = alpha * r2 + (1 - alpha) * grad_2**2
x1 -= (eta / np.sqrt(r1 + 1e-10)) * grad_1
x2 -= (eta / np.sqrt(r2 + 1e-10))* ( grad_2)
# print(f"x1 lr ", (eta / np.sqrt(r1 + 1e-10)))
# print(f"x2 lr ", (eta / np.sqrt(r2 + 1e-10)))
result.append((x1, x2))
plt.figure(figsize=(8, 4))
plt.plot(*zip(*result), "-o")
x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
C = plt.contour(x1, x2, loss_func(x1, x2), colors="red")
plt.clabel(C, inline=True, fontsize=10)
# ax1 = plt.axes(projection='3d')
# ax1.scatter3D(x1, x2, loss_func(x1, x2), cmap='Blues')
plt.show()