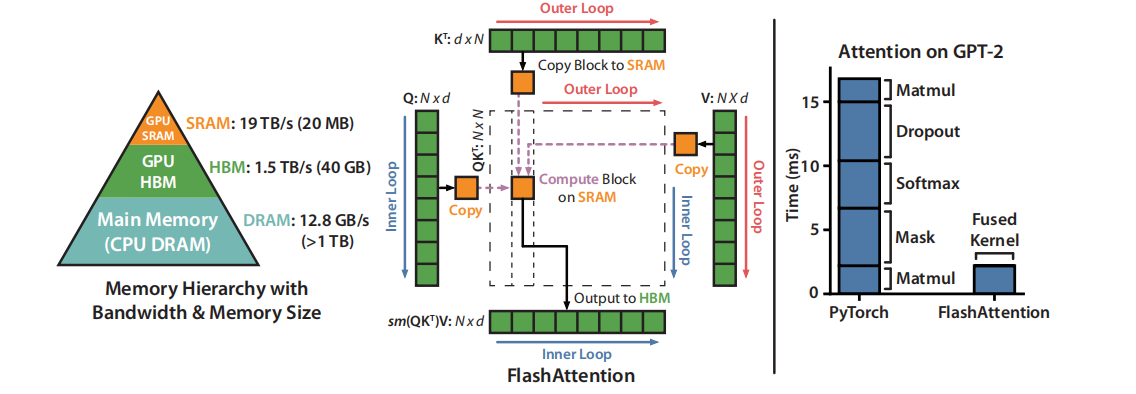
FlashAttention是一种利用软硬件加速结合非常好的算法,目前已经大幅度应用在模型的预训练过程中。
 分为4步计算:
分为4步计算:
 既然是由于Self-Attention计算来回重复在HBM和SRAM之间存储数据导致的Memory延迟,那么我们总结了2点疑问和2点情况说明:
既然是由于Self-Attention计算来回重复在HBM和SRAM之间存储数据导致的Memory延迟,那么我们总结了2点疑问和2点情况说明:
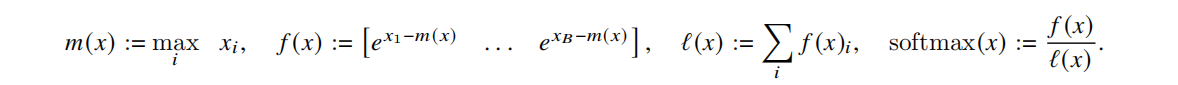 Oneline-Softmax:
Oneline-Softmax:
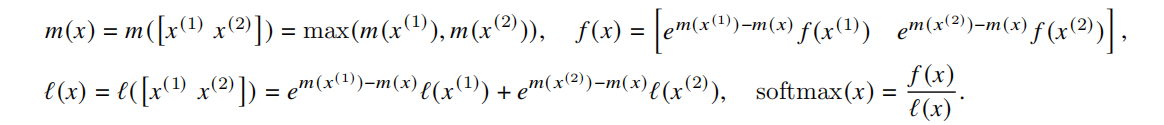

1 FlashAttention前置知识
在介绍FlashAttention算法之前我们先来介绍一些前置知识。 Memory:-
- SRAM > HBM > DRAM
- SRAM:Static RAM(Random Access Memory)
- 每个 SM(Stream multiproecssors,流多处理器)192KB (A100 108个,4090 128个)
- 108*192/1024 = 20MB
- 每个 SM(Stream multiproecssors,流多处理器)192KB (A100 108个,4090 128个)
- HBM:high bandwidth memory(4090 24GB,A100 80GB)
- compute-bound
- 运算的主要时间都耗费在 operation 的计算上,HBM 的存取只占了其中一点点的时间
- 像是多维度的矩阵相乘或是高 channel 数的 convolution 都属于这类。
- memory-bound
- 主要时间都耗费在 memory 的读取上,而实际的运算只占了其中一点点的时间
- elementwise (e.g., activation, dropout) and reduction (e.g., sum, softmax, batch norm, layer norm)
- 现象:在GPU当中有非常大量的 threads (kernel) 负责执行 operation 的运算,而整个运算的过程基本上是从 HBM 当中将资料加载至 SRAM 中,执行运算并将 output 存回 HBM 当中。
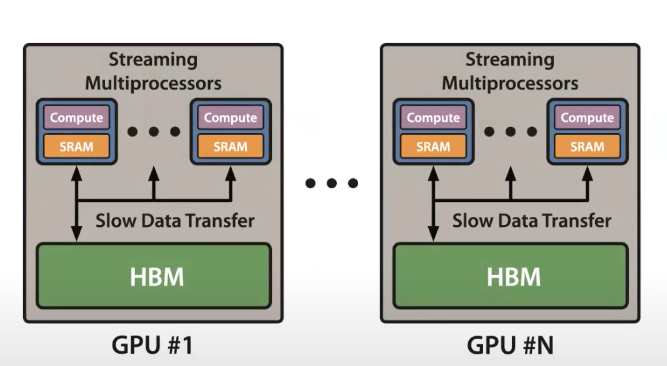
- 解决办法:operations fused
- 将好几个 operations fuse 成一个 operation 进而减轻 memory 存取的 loading
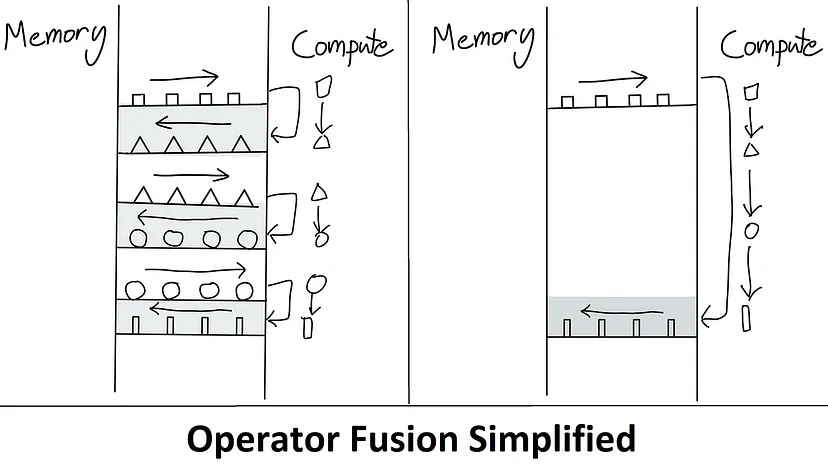
- 代码示例:
-
# 独立的内核调用 a = x + y # 内核1 b = a * z # 内核2 c = torch.relu(b) # 内核3 # 优化后的内核(操作融合为一个内核) # 定义操作融合的内核(使用 TorchScript) @torch.jit.script def fused_kernel(x, y, z): a = x + y b = a * z c = torch.relu(b) return c
- 将好几个 operations fuse 成一个 operation 进而减轻 memory 存取的 loading
2 Self-Attention
Self-Attention的计算如下图:O = Dropout(Softmax(QK^T))V 分为4步计算:
分为4步计算:
- QK^T -> Softmax -> Dropout -> PV
- compute-bound:QK^T + PV
- memory-bound:Softmax + Dropout
 既然是由于Self-Attention计算来回重复在HBM和SRAM之间存储数据导致的Memory延迟,那么我们总结了2点疑问和2点情况说明:
既然是由于Self-Attention计算来回重复在HBM和SRAM之间存储数据导致的Memory延迟,那么我们总结了2点疑问和2点情况说明:
- 疑问1: 上图我们发现,为了得到计算结果O,我们需要计算中间值S和P,中间值S和P一定是必要的嘛?
- 疑问2:既然融合计算可以减少HBM到SRAM的操作,进而减少memory交换时间,为什么不可以将Softmax(QK^T)直接搬到SRAM中进行融合计算。
- 情况1:需要S和P作为中间激活值用来反向传播
- 情况2:SRAM不够大无法同时执行Softmax(QK^T)这么大的操作
- 1 针对情况1,我们抛弃S和P,让其在反向传播时重新计算
- 2 对矩阵QKV做分块,分块后Softmax(QK^T)足够全部放到SRAM中执行,但是传统的Softmax不支持分块计算,online-softmax的舞台来了
3 FlashAttention
3.1 Tiling
3.1.1 Softmax & Online-Softmax
Online-softmax让Tiling分块操作成为了现实 -> 让融合计算成为了现实。 Self-Attention计算Softmax: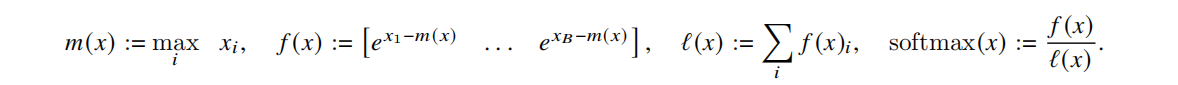 Oneline-Softmax:
Oneline-Softmax:
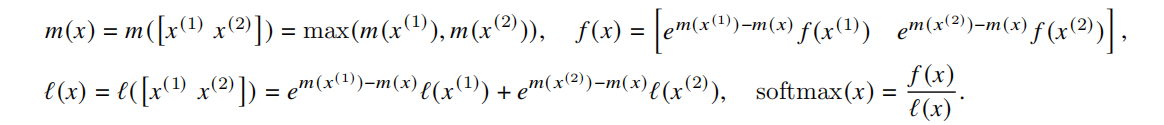
3.1.2 FlashAttention算法图示

3.1.3 FlashAttention伪代码
